Para hallar la respuesta a todas estas preguntas tenemos que comparar conjuntos infinitos de números ;hallar si en estos conjuntos hay la misma cantidad de números o no.¿Y cómo se hace ésto?Se ha de emparejar cada elemento del primer conjunto con cada elemento del segundo conjunto sin que sobre ninguno,ya que si sobrase alguno no tendría el mismo número de elementos y ,por tanto,los infinitos no serían todos iguales.
- Comparemos los nºnaturales y los nº enteros
N
|
1
|
2
|
3
|
4
|
5
|
6
|
7
|
8
|
…
|
Z
|
0
|
1
|
-1
|
2
|
-2
|
3
|
-3
|
4
|
…
|
- Comparemos los nº naturales con los nº racionales
Numerador : 1 2 3 4 5 ...
1/1
|
2/1
|
3/1
|
4/1
|
5/1
|
..
|
1/2
|
2/2
|
3/2
|
4/2
|
..
|
..
|
1/3
|
2/3
|
3/3
|
..
|
..
|
..
|
1/4
|
2/4
|
..
|
..
|
..
|
..
|
1/5
|
..
|
..
|
..
|
..
|
..
|
..
|
..
|
..
|
..
|
..
|
..
|
Si quitamos las fracciones repetidas, podemos proceder al emparejamiento de N con los racionales positivos:
N
|
1
|
2
|
3
|
4
|
5
|
6
|
7
|
8
|
…
|
Q+
|
0
|
1/1
|
2/1
|
1/2
|
1/3
|
3/1
|
4/1
|
3/2
|
…
|
Para emparejar N con todo Q se mantiene la tabla anterior cambiando la fila superior por los números pares y añadir los naturales impares emparejados a los racionales negativos .
N
|
1
|
2
|
3
|
4
|
5
|
6
|
7
|
8
|
9
|
10
|
11
|
…
|
Q
|
0
|
1/1
|
-1/1
|
2/1
|
-2/1
|
1/3
|
-1/3
|
3/1
|
-3/1
|
4/1
|
-4/1
|
…
|
Otra manera de demostrarlo es con el Árbol de Calkin-Wilf:
Expresaremos cualquier nºnatural como suma de potencias de base 2,pero con la condición de que cada potencia aparezca a lo sumo 2 veces.Expresamos todas las posibilidades.
Llamaremos S(n) al número de maneras de expresar  como suma de potencias de 2 con la condición anterior.
como suma de potencias de 2 con la condición anterior.
El 1 se puede escribir de una forma, el 2 de dos, el 3 de una …Si colocamos en fila los valores de  , para
, para  , definiendo
, definiendo  como 1, obtenemos la siguiente lista:
como 1, obtenemos la siguiente lista:
Tomamos los cocientes de cada dos términos consecutivos de esta sucesión,obteniendo:
Propiedades:
- El denominador de cada fracción es el numerador de la siguiente.
- Al ser cada elemento de la sucesión
primo relativo con
, todas las fracciones en esta lista son irreducibles
- Y lo que es más sorprendente, todo nºracional positivo aparece solamente una vez en esta sucesión,por lo que hay tantas fracciones como nº naturales.

Comienza con el nº 1.Cada fracción
Demostración de las propiedades:
- El numerador y el denominador de cada fracción son primos relativos
 es el mismo que el cardinal de
es el mismo que el cardinal de  , esto es,
, esto es,  .
.
Supongamos que existe alguna fracción del árbol para la que ésto no es cierto. De entre todas las que no cumplen esta propiedad, tomemos la que aparece más arriba en este árbol, digamos  . a y b tienen factores comunes.
. a y b tienen factores comunes.
Esta fracción será ''hija'' de la fracción que tiene justo en el nivel anterior. Si es la de la izquierda, entonces proviene de la fracción 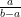 , que entonces también cumpliría que su numerador y su denominador tienen factores comunes, lo que contradice que
, que entonces también cumpliría que su numerador y su denominador tienen factores comunes, lo que contradice que  era la fracción con esa característica que aparecía más arriba en el árbol. Si es la de la derecha proviene de la fracción
era la fracción con esa característica que aparecía más arriba en el árbol. Si es la de la derecha proviene de la fracción  , con lo que aplicando el mismo razonamiento,llegaríamos a la misma conclusión.
, con lo que aplicando el mismo razonamiento,llegaríamos a la misma conclusión.
Por tanto, todas las fracciones que aparecen en el árbol son irreducibles.
-Ningún número racional aparece más de una vez
Supongamos entonces que hay fracciones que aparecen más de una vez en el árbol. Tomamos la que tenga menor denominador como  . Si
. Si  , entonces
, entonces  es el hijo de la izquierda de al menos dos números racionales distintos (ya que al menos aparece dos veces en el árbol), siendo ambos la fracción
es el hijo de la izquierda de al menos dos números racionales distintos (ya que al menos aparece dos veces en el árbol), siendo ambos la fracción 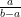 , hecho que contradice que
, hecho que contradice que  era la fracción de menor denominador entre las que aparecen más de una vez. De forma parecida se demuestra para
era la fracción de menor denominador entre las que aparecen más de una vez. De forma parecida se demuestra para  .
.
Por tanto ,el cardinal* de
*Cardinal:número de elementos de un conjunto- Todo número racional positivo aparece en algún vértice
Al infinito referido a los números naturales se le llama אּ0 (Aleph sub cero). Los conjuntos que se pueden emparejar con los naturales decimos que son numerables.
 , que establece una biyección entre el intervalo
, que establece una biyección entre el intervalo  y el intervalo
y el intervalo  . Es bien sencillo demostrar que esta función es biyectiva, es decir, que pone en correspondencia uno a uno a esos dos intervalo.
. Es bien sencillo demostrar que esta función es biyectiva, es decir, que pone en correspondencia uno a uno a esos dos intervalo.
 . Esta función es una biyección entre el intervalo
. Esta función es una biyección entre el intervalo  y
y  , es decir, pone en correspondencia biunívoca ese intervalo con el conjunto de los números reales.
, es decir, pone en correspondencia biunívoca ese intervalo con el conjunto de los números reales.
 , decimos que el cardinal de
, decimos que el cardinal de 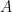 es menor que el cardinal de
es menor que el cardinal de  ,
, 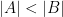 (
( representa el cardinal de
representa el cardinal de 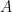 ), si podemos poner en correspondencia biunívoca el conjunto
), si podemos poner en correspondencia biunívoca el conjunto 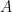 con un subconjunto de
con un subconjunto de  y no podemos hacer lo mismo entre
y no podemos hacer lo mismo entre 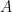 y
y  .
.
·Aclaración:


 (el cardinal de R>cardinal de N ,por lo que R es un conjunto no numerable)
(el cardinal de R>cardinal de N ,por lo que R es un conjunto no numerable)
El número racional 1 aparece en el comienzo del árbol.
Supongamos que hay números racionales que no aparecen en ningún vértice. Tomemos como  la que tenga menor denominador de entre todos ellos. Si
la que tenga menor denominador de entre todos ellos. Si  , la fracción
, la fracción  tampoco aparecería en el árbol (ya que si lo hiciera entonces también aparecería
tampoco aparecería en el árbol (ya que si lo hiciera entonces también aparecería  ), pero
), pero  tiene numerador menor que
tiene numerador menor que  , teniendo ambas el mismo denominador, hecho que contradice la suposición inicial. De forma análoga se llega a una contradicción con
, teniendo ambas el mismo denominador, hecho que contradice la suposición inicial. De forma análoga se llega a una contradicción con  .
.
- Comparemos los nº naturales con los reales
Lema:
El cardinal del intervalo  es el mismo que el cardinal de
es el mismo que el cardinal de  .
.
Demostración:
La idea de la demostración es encontrar una función que pongan en correspondencia uno a uno el intervalo  con
con  . Este tipo de funciones se llaman biyectivas.
. Este tipo de funciones se llaman biyectivas.
La función que buscamos es composición de dos:
Realizando la composición de las dos obtenemos una biyección entre el intervalo  y
y  . Por tanto ambos conjuntos tienen el mismo cardinal.
. Por tanto ambos conjuntos tienen el mismo cardinal.
La idea ahora es demostrar que el infinito de los números reales es mayor que el de los naturales. Para ello veremos que el cardinal de estos últimos es menor que el de los primeros. Pero antes vamos a dar una definición sobre esto que nos va a echar una mano:
·Aclaración:
No basta con quepueda ponerse en correspondencia uno a uno con un subconjunto de
para decir que
. La segunda condición es obligatoria para que la definición tenga sentido. Un ejemplo claro de esto es la relación entre los números pares y todos los números naturales: los números pares pueden ponerse en correspondencia biunívoca con un subconjunto de los naturales (de hecho con varios: los propios números pares, los impares,...), pero sabemos ya que los números pares también pueden ponerse en correspondencia uno a uno con los propios números naturales, por lo que el cardinal de los pares es el mismo que el de los naturales.Recordando que dijimos que un conjunto infinito es numerable si puede ponerse en correspondencia biunívoca con los naturales, presentamos el enunciado del teorema de Cantor(método diagonal):
El conjunto de los números reales,  , no es numerable, es decir,
, no es numerable, es decir,  .
.
Demostración
La idea es utilizar la definición anterior. Por ello lo primero que debemos hacer es encontrar un subconjunto de  que pueda ponerse en correspondencia uno a uno con
que pueda ponerse en correspondencia uno a uno con  . Ese subconjunto va a ser el propio
. Ese subconjunto va a ser el propio  , que como sabemos es un subconjunto de los reales. Ya tenemos entonces la primera parte:podemos poner en correspondencia biunívoca*** a
, que como sabemos es un subconjunto de los reales. Ya tenemos entonces la primera parte:podemos poner en correspondencia biunívoca*** a  con un subconjunto de
con un subconjunto de  .
.
***Correspondencia biunívoca:cada elemento del primer conjunto se corresponde con solo un elemento del segundo conjunto, y cada elemento del segundo conjunto se corresponde con solo un elemento del primer conjunto.)
Según el resultado demostrado anteriormente tenemos que  . Por ello si demostramos que
. Por ello si demostramos que  ya tendremos que
ya tendremos que  . Para ello vamos a suponer que tenemos una correspondencia cualquiera entre
. Para ello vamos a suponer que tenemos una correspondencia cualquiera entre  y
y  y encontraremos un elemento de
y encontraremos un elemento de  que no se corresponde con ninguno de
que no se corresponde con ninguno de , es decir, veremos que no hay correspondencias uno a uno entre esos dos conjuntos.
, es decir, veremos que no hay correspondencias uno a uno entre esos dos conjuntos.
Cualquier correspondencia biunívoca entre  y
y  es básicamente una numeración de los elementos de
es básicamente una numeración de los elementos de  , es decir, creamos una lista con los elementos de ese intervalo, digamos
, es decir, creamos una lista con los elementos de ese intervalo, digamos  , y asociamos cada número natural con uno de esos elementos. Cada uno de ellos será un cero seguido de un cierto número (finito o infinito) de decimales. Evitando repeticiones (ya sabemos que
, y asociamos cada número natural con uno de esos elementos. Cada uno de ellos será un cero seguido de un cierto número (finito o infinito) de decimales. Evitando repeticiones (ya sabemos que  y
y  son el mismo número) tendríamos algo así:
son el mismo número) tendríamos algo así:
La clave es la siguiente: vamos a encontrar un elemento del intervalo  que no corresponde con ningún número natural. Para ello tomamos
que no corresponde con ningún número natural. Para ello tomamos  y nos quedamos con su primer decimal, al que sumamos 1 obteniendo
y nos quedamos con su primer decimal, al que sumamos 1 obteniendo  ; tomamos ahora
; tomamos ahora  y nos quedamos con su segundo decimal, sumándole también 1, obteniendo
y nos quedamos con su segundo decimal, sumándole también 1, obteniendo  ; y así sucesivamente (si alguno de ellos es un 9 ponemos un cero). Ahora formamos el número
; y así sucesivamente (si alguno de ellos es un 9 ponemos un cero). Ahora formamos el número 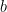 siguiente:
siguiente:
Para que se entienda mejor pongo el siguiente ejemplo:
Si tenemos las siguientes relaciones:
construiríamos.
Es evidente que, construido así,  y también es claro que
y también es claro que 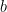 no corresponde con ningún número natural, ya que difiere con
no corresponde con ningún número natural, ya que difiere con  en (al menos) el primer decimal, con
en (al menos) el primer decimal, con  en (al menos) el segundo, con
en (al menos) el segundo, con  en (al menos) el tercero…
en (al menos) el tercero…
Hemos encontrado entonces un elemento del intervalo  que no corresponde con ningún número natural en cualquier correspondencia que podamos crear entre estos dos conjuntos. Por tanto
que no corresponde con ningún número natural en cualquier correspondencia que podamos crear entre estos dos conjuntos. Por tanto  y, en consecuencia:
y, en consecuencia:
Por tanto,hay infinito es un concepto ,ya que no todos los infinitos son iguales,hay infinitos mayores que otros.
REALIZADO POR:Candela Silvana Portilla Schachter
REALIZADO POR:Candela Silvana Portilla Schachter
No hay comentarios:
Publicar un comentario