Newton fuè el primero en demostrar que las leyes naturales que gobiernan el movimiento en la Tierra y las que gobiernan el movimiento de los cuerpos celestes son las mismas.
Fuè físico, filósofo, teólogo, inventor, alquimista, matemático inglés y autor de grandes obras.
Entre uno sus descubrimientos científicos se destacan los trabajos sobre la naturaleza de la luz y la óptica (que se presentan principalmente en su obra Opticks) y el desarrollo del cálculo matemático.
El matemático y físico matemático Joseph Louis Lagrange (1736–1813), dijo que:
"Newton fue el más grande genio que ha existido y también el más afortunado dado que sólo se puede encontrar una vez un sistema que rija el mundo."
Tras esta introducción general y breve comenzaré hablando acerca de su biografía, a continuación explicaré cómo se formó este gran genio, luego hablaré de sus rasgos más ctos así como la parte más relacionada con mis conocimientos, es decir el Newton matemático, y finalmente hablaré acerca de uno de sus descubrimientos más importantes y curiosos.
Isaac Newton nació el día de Navidad (25 de diciembre) de 1642 en Woolsthorpe, justamente el mismo día en que moría Galileo Galilei en Arcetri, a las afueras de Florencia. Ello dio lugar a que el filósofo inglés Bertrand Russel bromeara, tres siglos después, sobre esta circunstancia apoyando la teoría de la transmigración de las almas.
El científico Isaac Newton (1642-1727) es uno de los más importantes e influyentes de la historia de la ciencia, llamado padre de la ciencia moderna.
LOS AÑOS DE FORMACIÓN
Nacido prematuramente el día de Navidad, el mismo año de la muerte de Galileo, Newton fue un niño tan enclenque y débil que no se creyó que pudiera sobrevivir. Su padre, propietario rural, murió antes de su nacimiento, y su madre contrajo nuevas nupcias con Barnas Smith, rector de North Witham. El niño fue confiado, a la edad de tres años, a su abuela, que le hizo cursas sus primeros estudios en las escuelas primarias de Skilington y de Stoke, dos aldeas cercanas a Woolsthorpe. A los doce años fue enviado a la escuela pública de Grantham, alojándose en casa del farmacéutico del lugar. Él mismo contará, más tarde, que era un alumno muy poco atento que prefería divertirse construyendo máquinas, tales como una especie de clepsidra, muy precisa, un cuadrante solar, y un molino accionado por un ratón, a quien llamaba “el molinero” y que, para comer, se apartaba una cierta cantidad de la propia harina que producía. Le gustaba también dibujar del natural o de modo imaginativo, y tenía las paredes de su habitación llenas de dibujos y pinturas.
Vuelta a enviudar en 1656, su madre le reclamó desde Woolsthorpe, a fin de emplearlo en la administración y los trabajos de su finca. Pero al joven Newton no le interesaba este tipo de ocupación, y así, mientras un antiguo sirviente de la casa se ocupaba de las compras y las ventas que le habían encargado a él, en el mercado de Grantham, Newton volvía a casa de su antigua patrón para entregarse a la lectura de viejos libros, o se paraba, incluso, en pleno camino, y era tal la pasión que demostró para el estudio de las ciencias que, previa la intervención de un tío suyo, le valió la prosecución de sus estudios en Grantham. Más tarde, a los dieciocho años, se matriculó en el Trinity College de Cambridge, donde fue rápidamente distinguido por su profesor, el matemático Isaac Barrow (1630-1677), obteniendo, en 1665, su título de bachiller en artes.
Los años más productivos de Newton fueron de 1665 a 1666, en los que la Universidad de Cambridge cerró por 18 meses debido a que la peste bubónica azotaba Inglaterra y Newton, un estudiante de la Universidad, se fue a la granja de su familia donde no pudo hablar de Ciencia con nadie, pero donde sus únicos pensamientos le llevaron a la invención del cálculo, el descubrimiento de la gravitación universal y otros descubrimientos más pequeños.
Frases de Newton:
1-"Lo que sabemos es una gota de agua; lo que ignoramos es el océano."
2-"Los hombres construimos demasiados muros y no suficientes puentes."
3-"Si he hecho descubrimientos invaluables ha sido más por tener paciencia que cualquier otro talento."
4-"Si consigo ver más lejos es porque he conseguido auparme a hombros de gigantes."
5-"La unidad es la variedad, y la variedad en la unidad es la ley suprema del universo."
6-" No se lo que pareceré a los ojos del mundo, pero a los míos es como si hubiese sido un muchacho que juega en la orilla del mar y se divierte de tanto en tanto encontrando un guijarro más pulido o una concha más hermosa, mientras el inmenso océano de la verdad se extendía, inexplorado frente a mi."
7-"A falta de otra prueba, el dedo pulgar por sí solo me convencería de la existencia de Dios."
8-"El tacto es el arte de hacer un punto sin hacer un enemigo."
9-"La naturaleza es verdaderamente coherente y confortable consigo misma."
10-"Si he hecho descubrimientos invaluables ha sido más por tener paciencia que cualquier otro talento."
11-"Si consigo ver más lejos es porque he conseguido auparme a hombros de gigantes."
12-"Las mujeres cuanto mas masa tengan, mas atractivas son."
13-"Puedo calcular el movimiento de los cuerpos celestes, pero no la locura de la gente."
14-"Dios es capaz de crear partículas de materia de distintos tamaños y formas...Y quizás de densidades y fuerzas distintas, y de este modo puede variar las leyes de la naturaleza, y hacer mundos de tipos diferentes en partes diferentes del universo. Yo por lo menos no veo en esto nada contradictorio."
15-"Este bellísimo sistema compuesto por el Sol, los planetas y los cometas no pudo menos que haber sido creado por consejo y dominio de un ente poderoso e inteligente... El Dios Supremo es un Ser eterno, infinito, absolutamente perfecto.
Finalmente hablaremos del binomo de Newton:
Isaac Newton generalizó la fórmula para tomar otros exponentes, considerando una serie infinita:
Donde r puede ser cualquier número complejo (en particular, r puede ser cualquier número real, no necesariamente positivo ni entero), y los coeficientes están dados por:

(el k = 0 es un producto vacío y por lo tanto, igual a 1; en el caso de k = 1 es igual a r, ya que los otros factores (r − 1), etc., no aparecen en ese caso).
Una forma útil pero no obvia para la potencia recíproca:
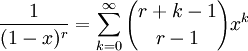
La suma en converge y la igualdad es verdadera siempre que los números reales o complejos x e y sean suficientemente cercanos, en el sentido de que el valor absoluto | x/y | sea menor a uno.
Calcular Binomio
Para calcular un Binomio de Newton estilo  podemos hacer de forma sencilla:
podemos hacer de forma sencilla:  REALIZADO POR: ADRIÁN TAPIADOR
REALIZADO POR: ADRIÁN TAPIADOR





















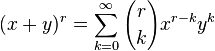

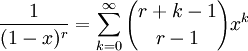
 podemos hacer de forma sencilla:
podemos hacer de forma sencilla: